Suite à un petit fil twitter :
on tente une implémentation de la formule de Bauer.
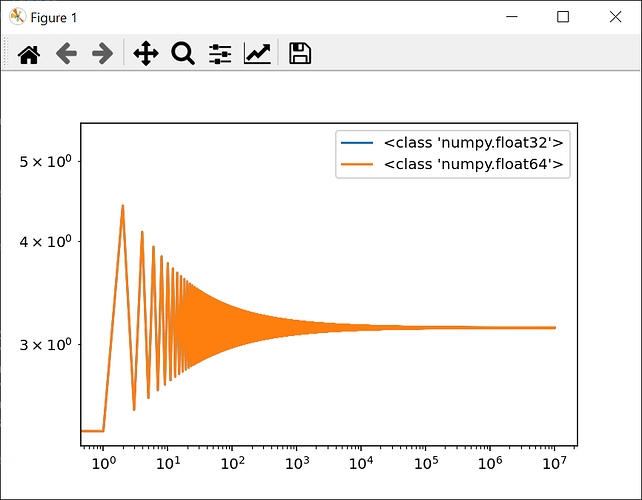
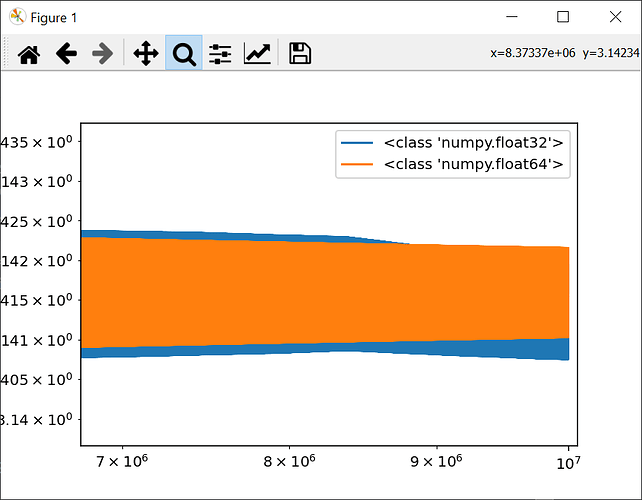
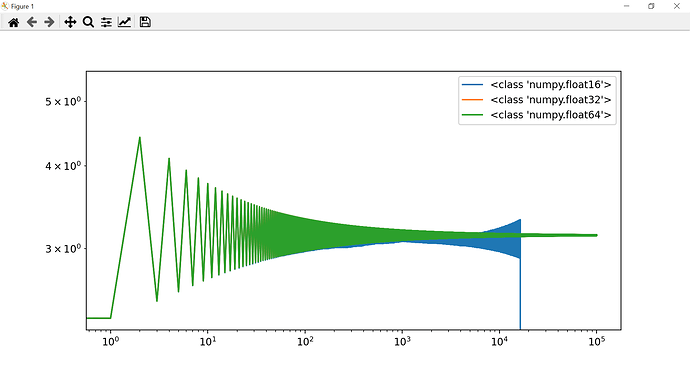
Twitter était parti sur le préjugé que les floats posaient un problème, et faisaient converger la série trop lentement, mais après quelques tests je n’ai vraiment pas l’impression que ce soit le cas, typiquement pour 5000 itérations soit on obtient :
3.116726637964121
soit on obtient :
Decimal('3.116726637964128607889625792'))
et heureusement, car num et dem grossissent très vite, et instantier des Decimal de ces valeur pour les diviser prend un temps faramineux.
Mon implémentation actuelle est :
from collections import deque
from statistics import mean
from time import perf_counter
from itertools import count
def bauer():
s = 0
num = den = 1
for k in count(1):
f1 = (-1) ** k
f2 = 4 * k + 1
num *= 2 * k - 1
den *= 2 * k
product = f1 * f2 * ((num / den) ** 3)
s += product
yield 2 / (1 + s)
start = perf_counter()
last_values = deque([0, 0], 2)
for n, pi in enumerate(bauer(), start=1):
last_values.append(pi)
if n % 1000 == 0:
print(pi, f"for {n} iterations", "after", perf_counter() - start, "s")
print(f" (average={mean(last_values)}")
Je fait la moyenne des deux dernières valeurs car j’ai remarqué que l’approximation tapait alternativement en dessus et en dessous de la cible, ça commence à rendre quelque chose de potable:
[...]
3.1376244069088823 for 199000 iterations after 130.45243947894778 s
(average=3.1415976837087083
3.1376343274048155 for 200000 iterations after 131.82237681292463 s
(average=3.141597658545669
[...]
3.1404938090140138 for 2600000 iterations after 30536.77467655996 s
(average=3.141593038310659
3.1404940201954075 for 2601000 iterations after 30561.442449155962 s
(average=3.14159303816273
3.1404942312550688 for 2602000 iterations after 30584.007838679012 s
(average=3.1415930380149075
[...]